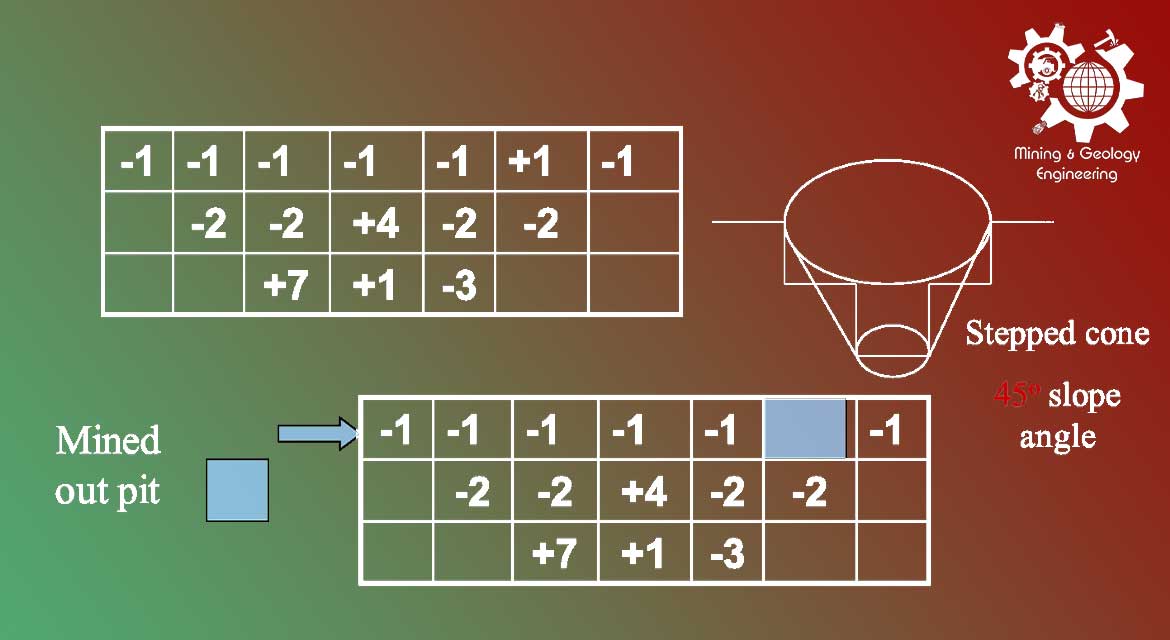
طراحی معدن به روش مخروط شناور اصلاح شده
قبل از استخراج موادمعدنی به روش روباز، لازم است که اندازه و شکل نهایی معدن به منظور تعیین میزان ذخیره قابل استخراج و میزان باطله برداری و همچنین تعیین محل سد باطله و دیگر تاسیسات سطحی، طراحی شود. محدودۀ معدن تابع پارامترهای مختلفی میباشد که ممکن است در طول عمر معدن، بدلیل تغییر این پارامترها چندین بار بازنگری شود. بنابرین استفاده از کامپیوتر برای طراحی مجدد در کوتاهترین زمان ممکن ضروری است.
پس از اختراع کامپیوتر و استفاده همه جانبه آن، الگوریتمهای مختلفی نظیر روش مخروط شناور، روش گراف تئوری لرچ و گروسمن و. . جهت طراحی محدودۀ بهینه نهایی معرفی شده است. از میان این الگوریتمها، روش گراف تئوری لرچ و گروسمن تنها روشی است که قادر است محدودۀ بهینه واقعی را در تمام مدلها محاسبه نماید. پیچیدگی این روش و نیاز به وقت کامپیوتری بالا جهت حصول به جواب از معایب روش مذکور میباشد.
روش مخروط شناور به دلیل اینکه در مدت زمان کمتری قادر است محدودۀ بهینه را محاسبه نماید و همچنین به دلیل سادگی، از سایر الگوریتمها بیشتر استفاده میشود. این الگوریتم در بعضی از حالات قادر به تعیین محدودۀ بهینه نیست. به همین دلیل روش مخروط شناور دو برای بر طرف نمودن بعضی از معایب روش مذکور توسط رایت ارائه و ادعا شده است که این روش قادر به تعیین محدودۀ بهینه واقعی میباشد.
قبل از استخراج مواد معدنی به روش روباز، لازم است که اندازه و شکل محدودۀ نهایی معدن جهت تعیین میزان ذخیره قابل استخراج و مقدار باطله برداری، طراحی برنامهریزی تولید و تعیین محل دیگر تاًسیسات سطحی نظیر مسیرهای دسترسی، دپوی باطله، کارخانههای فرآوری تعیین گردد.
محدودۀ معدن که تابع پارامترهای مختلفی نظیر عیار مادهمعدنی، عیار حد، هزینههای استخراج، باطلهبرداری و فرآوری، راندمان و قیمت مادهمعدنی میباشد ممکن است در طول عمر معدن بدلیل تغییر این پارامترها و یا کسب اطلاعات اکتشافی جدید چندین بار بازنگری شود. بنابر این استفاده از کامپیوتر جهت طراحی معدن ضروری است.
برای تعیین محدودۀ معدن روشهای مختلفی استفاده میشود. این روشها را میتوان به سه دسته کلی شامل طراحی دستی، طراحی کامپیوتری و طراحی بهینه تقسیم نمود. از میان اینها روشهای طراحی بهینه که بر اساس الگوریتمهای مشخصی محدودۀ نهایی معادن روباز را تعیین میکنند از اهمیت خاصی برخوردار است. استفاده از کامپیوتر برای طراحی بهینه محدودۀ معادن روباز معمولا” با ساختن یک مدل بلوکی از کانسار شروع میشود. برای این منظور ابتدا ذخیره به صورت یک بلوک بزرگ در نظر گرفته میشود به طوری که تمام نواحی کانهسازی شده را دربر گیرد. سپس در مرحله بعد آنرا به بلوکهای کوچکتر تقسیم نموده و به هر کدام عیار تخمینی کانه یا ارزش آن اختصاص داده میشود.
بلوکهای مذکور ممکن است شکل و ابعاد مختلفی داشته باشند. مدلهای بلوکی کانسار با توجه به تقسیم آن به بلوکهای کوچکتر، مدل سه بعدی منظم، سه بعدی نا منظم، دو بعدی منظم و دو بعدی نامنظم گویند که از میان اینها مدل سهبعدی منظم که در آن تمام بلوکها به یک اندازه هستند استفاده بیشتری دارد. ارتفاع بلوکها در این مدل را معمولا” به اندازه ارتفاع طراحی شده پله در نظر میگیرند ولی ابعاد افقی آنها بستگی به اطلاعات اکتشافی و فواصل نمونهبرداری دارد. طراحی بهینه محدودۀ نهایی در معادن روباز موضوعی است پیچیده که مستلزم انجام محاسبات بسیاری میباشد.
پس از اختراع و توسعه همه جانبه کامپیوتر الگوریتمهای زیادی جهت تعیین محدودۀ بهینه معادن روباز معرفی شده که هدف اصلی همه آنها پیدا کردن مجموعه بلوکهایی است که اگر استخراج شوند سود بدست آمده تحت محدودیتهای فنی و اقتصادی حداکثر شود. مهمترین الگوریتمهای طراحی بهینه محدوده نهائی در معادن روباز عبارتند از: روش مخروط شناور، روش برنامهریزی پویا ، الگوریتم کوروبوف، روش لرچ و گروسمن، روش گراف تئوری
در سال ۱۹۹۹ برای بر طرف کردن بعضی ضعفهای روش مخروط شناور از روش مخروط شناور اصلاحی اولین بار توسط رایت معرفی گردید. بر طبق ادعای نامبرده، روش مذکور در عین سادگی قادر به تعیین محدودۀ بهینه واقعی در معادن روباز میباشد بدون اینکه ادعای مذکور به اثبات برسد.
روشهای مختلف مخروط شناور
روشهای مختلف مخروط شناور سادهترین راهحل را برای تعیین محدودۀ بهینه معادن روباز ارائه میدهد که در سال ۱۹۶۶ توسط کارلسون توضیح داده شده است. در این روش برای هر بلوک مثبت (ماده معدنی) یک مخروط معکوس با توجه به زاویه شیب پایداری معدن طوری ساخته میشود که راس آن در بلوک ماده معدنی باشد.
سپس ارزش بلوکهای واقع در داخل مخروط را با هم جمع کرده و در صورتی که نتیجه مثبت باشد تمام بلوکهای واقع در داخل آن جزء، محدودۀ معدن در نظر گرفته میشوند. در غیر این صورت جستجو برای بلوکهای مثبت دیگر ادامه مییابد. در این روش، جستجو برای بلوکهای مادهمعدنی از طبقه اول شروع شده و به طرف طبقات پایینتر ادامه مییابد. گرچه این روش بسیار ساده است و تهیه برنامه کامپیوتری آن نیز آسان میباشد ولی این الگوریتم قادر نیست در بعضی از مدلها محدودۀ بهینه را پیدا نماید.
روش لرچ و گروسمن
این روش که بر اساس نظریه گرافها استوار است در سال ۱۹۶۵ توسط لرچ و گروسمن معرفی گردید و تنها روشی است که ثابت شده است در همه حالات محدودۀ بهینه واقعی را بدست میآورد. روش مذکور مدل بلوکی اقتصادی کانسار را به یک گراف مستقیم تبدیل مینماید که در آن هر بلوک با گره و ارتباط بین آنها با بردار طوری نشان داده میشود که نمایانگر یک پیت قابل اجرا باشد.
در گراف مذکور مجموعهای از گرهها را که با توجه به شیب پایداری معدن می تواند تشکیل یک پیت قابل اجرا را نماید کلوژر میگویند. هر کلوژر دارای ارزشی است که برابر مجموع ارزش گرههای (بلوکهای) داخل آن است. لذا این الگوریتم با استفاده از یک سری قواعد سعی میکند که کلوژر یا پیت با بیشترین ارزش اقتصادی را پیدا نماید. مهمترین مزیت این روش قابلیت آن برای پیدا کردن محدودۀ بهینه واقعی معادن روباز در همه حالات است. معایب آن عبارتند از:
- پیچیدگی روش: یکی از انتقاداتی که بر این روش وارد شده است پیچیدگی الگوریتم و همچنین مشکل بودن تهیه برنامه کامپیوتری آن است که از عهده یک مهندس معدن بادانش متوسط خارج است. خیلی ها این انتقاد را وارد ندانسته و اظهار داشتهاند در صورت تهیه نرم افزار صحیح بر اساس این روش نیاز به دانستن جزئیات آن نیست.
- صرف وقت کامپیوتری زیاد برای حصول به جواب: در این شکی نیست که این روش با مقایسه با روشهای دیگر نیاز به صرف مدت زمان زیاد وقت کامپیوتر برای رسیدن به جواب دارد. به همین دلیل الگوریتمهای دیگری برای رفع این عیب معرفی گردیده است. در حال حاضر با توجه به پیشرفت سریع کامپیوتر، این عیب بزرگی نیست.
- مشکلات مربوط به استفاده از شیبهای متغیر: در محدودۀ معدن با توجه تنوع سنگهای مختلف و درزه و شکستگیها ممکن است شیب پایداری دیواره متغیر باشد. بنابراین الگوریتمهای طراحی بهینه بایستی قادر باشند محدودۀ معدن را با شیبهای متغیر طراحی نمایند. یکی دیگر از معایب این روش مشکل بودن اصلاح آن برای استفاده از شیبهای متغیر میباشد که کوششهای زیادی برای رفع آن صورت گرفته است. این مشکل نیز با طرح یک روش کلی پیشنهاد شده توسط نگارنده بر طرف گردیده و یک نرم افزار تحت ویندوز بر اساس روش مذکور و با شیبهای متغییر تهیه شده است لذا با توجه به معایب فوق، تحقیق و جستجو برای تهیۀ یک الگوریتم که در عین سادگی، بتواند محدودۀ بهینه واقعی را در زمان کم تعیین نماید توجیه پذیر است
روش مخروط شناور اصلاحی
روش مخروط شناور اصلاحی (دو) اولین بار در سال ۱۹۹۹ توسط رایت برای بر طرف کردن بعضی از ضعفهای روش مخروط ارائه شد و بر طبق ادعای نامبرده، روش مذکور قادر به تعیین محدودۀ بهینه واقعی در معادن روباز میباشد. الگوریتم این روش با انجام کمی تغییرات است. در این روش، شبیه روش مخروط شناور جستجو برای بلوکهای مادهمعدنی از طبقه اول شروع شده و به طرف طبقات پایینتر ادامه مییابد و برای هر طبقه عملیات زیر انجام میشود.
- برای هر بلوک مثبت (ماده معدنی) یک مخروط معکوس با توجه به زاویه شیب پایداری معدن طوری ساخته میشود که راس آن در بلوک مادهمعدنی باشد و سپس ارزش آن محاسبه میگردد.
- پس از اتمام محاسبۀ ارزش مخروط استخراجی تمام بلوکهای مادۀمعدنی در طبقۀ مورد بررسی، مخروط استخراجی با بالاترین ارزش را پیدا کرده و آن را جزء محدودۀ معدن فرض کرده و ارزش تجمعی پیت را محاسبه مینمایند
- پس از اصلاح مدل بلوکی اقتصادی قدمهای مذکور برای بقیه بلوکهای مثبت انجام میگردد. پس از انجام مراحل فوق بلوک با بالاترین ارزش تجمعی را پیدا کرده و در صورتی که مقدار آن مثبت باشد مخروطهای استخراجی برای این بلوک به محدودۀ بهینه اضافه میگردد
روش مخروط شناور اصلاحی گرچه این روش توانسته است بعضی از ضعفهای روش مخروط شناور را بپوشاند و نتایج بهتری نسبت به آن بدست آورد ولی با توجه بررسیهای مذکور این الگوریتم قادر نیست در بعضی از مدلها محدودۀ بهینه واقعی را پیدا نماید. علیرغم معایب مذکور این روش در مقایسه با روش لرچ و گروسمن دارای مزایای زیر است:
- روش مذکور در مدت کمتری محدودۀ بهینه را محاسبه مینماید.
- این روش بسیار ساده است و درک و فهم الگوریتم آن نیز آسان میباشد.
- استفاده از زاویۀ شیب متغیر در این روش به سهولت انجام میگیرد.
- تهیۀ برنامۀ کامپیوتری برای الگوریتم روش مذکور آسان میباشد.
اما جای پرسش است که چرا کار روی توسعه یک روش تعیین محدوده نهایی کارآمد هنوز هم ادامه دارد؟
یک پاسخ این است که خود مسئله تعیین محدوده نهایی تا این زمان هنوز به طور جامع مدل نشده است و از این رو تمام روشهای توسعه یافته برای حل مسأله با مدل کنونی به نوعی باز و ناتمام تلقی میشوند. در رایج ترین نگاه، این مسئله به صورت مجزا و به صورت مسئله استخراج کاواکی با ارزش بیشینه اقتصادی مطرح میشود. این در حالی است که این مدل گویای حقیقت مسئله نیست. تمام بلوکهای یک مدل در یک زمان استخراج نمیشوند و لذا باید ارزش اقتصادی تنزیل شده برای استخراج آنها در نظر گرفته شود؛ حال آنکه ارزش اقتصادی تنزیل شده تنها در صورتی قابل محاسبه است که شما پیش از آن محدوده نهایی و توالی استخراج را به دست آورده باشید. پس مسئله در یک دور ناتمام میافتد:
«محدوده کاواک با بالاترین ارزش خالص فعلی (NPV) قابل تعیین نیست مگر آن که ارزش بلوکها مشخص باشد؛ ارزش بلوکها قابل تعیین نیست مگر آن که توالی استخراج مشخص شده باشد و توالی استخراج قابل تعیین نیست مگر آن که محدوده کاواک معین شده باشد».
برای رفع این مشکل رویکردهای دیگری به مدلسازی و حل این مسئله مانند روش پارامتری کردن توسعه داده شدهاند که نارساییهای خود را دارند. با توجه به این که هنوز هیچ یک از این مدلها به طور کامل رد یا پذیرفته نشدهاند پس الگوریتمهای حل این مدلها نیز به صورت موازی پیش میروند.
روش الگوریتم کوروبوف اصلاح شده
الگوریتم کوروبوف در مواردی که مخروطهای استخراجی دارای بلوکهای مشترک باشند، گاه برای ارزیابی دچار خطا میشود. کوروبوف اصلاح شده برای رفع خطای الگوریتم اصلی کوروبوف یک قانون ساده اما کارآمد دارد:
«اگر دو یا چند مخروط دارای بلوکهای مشترک باشند، تخصیص ابتدا باید به بلوکهای غیرمشترک صورت پذیرد و تخصیص بلوکهای مشترک تنها زمانی انجام میشود که تمام مقادیر منفی بلوکهای غیرمشترک صفر شده باشد».
نکته بسیار مهم در فهم این شیوه این است که ماهیت نظری و اجرای عملی آن اندکی متفاوت است. ابداعکنندگان در مقاله سال ۱۹۹۲ در شرح ماهیت نظری این الگوریتم و رفتاری که در حالت آرمانی باید از خود نشان میدهد از نمودار موجود در شکل 1 استفاده کردهاند. در این شکل برای خلاصهسازی Ci نماد مخروطی است که روی i اُامین بلوک مثبت در طبقه مورد بررسی تشکیل میشود.
بر این اساس ماهیت نظری الگوریتم به این صورت است که هر بار یک ترکیب به ترتیب از میان گروههای زیر انتخاب میشود ( ابتدا C1 بعد C2 بعد C1&C2 بعد C3 و …) و بعد در هر موردی که بلوک مشترک در مخروط آن ترکیب وجود داشت، ابتدا تخصیص به بلوکهای غیرمشترک و سپس به بلوکهای مشترک صورت میپذیرد. اگر در پایان این فرآیند ارزش مخروط همچنان مثبت بود، مخروط به پاسخ اضافه میشود و در غیر این صورت پس از بازگرداندن مقادیر اصلی به بلوکها، جستجو به سراغ ترکیب دیگری میرود.
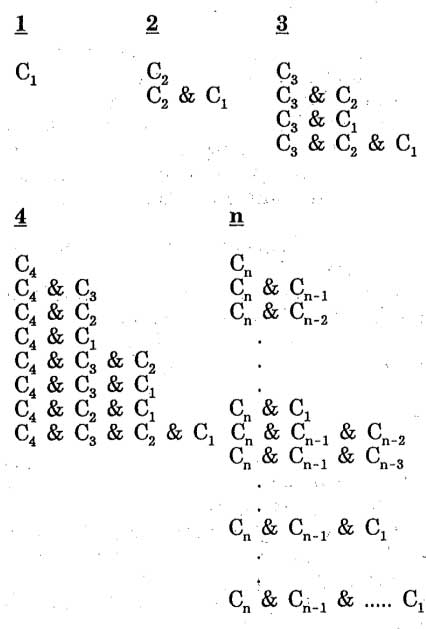
شکل 1 – چگونگی ترکیب و ترتیب بررسی گروههای مخروط استخراجی
این کاملترین نوع جستجو است که البته بدیهی است که در واقعیت نه انجام آن ضروری و نه در تمام موارد ممکن است. در مدلهای کوچک دوبعدی میتوان این روش را برای آموزش مفهوم الگوریتم به کار گرفت اما بررسی تمام ترکیبهای ممکن در یک مدل بلوکی بزرگ باعث کاهش کارایی به لحاظ مصرف حافظه و زمانبری میشود.
پس ابداعکنندگان یک راهکار عملی برای اجرای این الگوریتم معرفی کردند که توسط آن بسیاری از ترکیبهای ممکن پیش از بررسی عملا حذف شوند. در این روش در هر طبقه الگوریتم کوروبوف اصلی تا جایی اجرا میشودکه ارزش یک بلوک مثبت پس از تخصیص، مثبت باقی بماند. در این نقطه اجرای الگوریتم متفاوت میشود و به جای استخراج این بلوک، این موضوع بررسی میشود که آیا در مخروط مربوط به آن، بلوکی وجود دارد که توسط مخروط مجاوری از قبل مقداردهی شده باشد یا خیر.
اگر این طور نباشد که آن بلوک مثبت و مخروط آن خیلی ساده به جواب بهینه اضافه میشوند و اجرای الگوریتم کوروبوف در آن طبقه ادامه مییابد. اما اگر این طور باشد (یعنی بلوک مشترکی با یک مخروط مجاور یافت شود) در این صورت فرآیندی به نام بازتخصیص انجام میشود و تنها در صورتی که پس از این فرآیند، ارزش بلوک مورد نظر هنوز مثبت باشد مخروط استخراجی آن و تمام مخروطهایی که با این مخروط بلوک مشترک دارند، استخراج میشوند.
دقت کنید که در این شیوه، اجرای الگوریتم اصلاح شده تنها در پایان جستجوی یک طبقه مقادیر بلوکها به حالت نخست باز میگردد و جستجو از طبقه بعد ادامه مییابد (برخلاف الگوریتم کوروبوف که با استخراج یک بلوک مثبت و مخروط آن، ارزشها به حالت اول بازمیگشتند و جستجو از آخرین بلوک مثبت ناکام قبلی از سرگرفته میشود)؛ پس در هیچ حالت دیگری جز تغییر طبقه، مقادیر به حالت اولیه بازنمیگردند.
روش اجرای الگوریتم در قالب یک روندنما در مقاله سال ۱۹۹۳ ابداعکنندگان آورده شده است.
موضوع مهم در مورد الگوریتم کوروبوف اصلاح شده، معرفی نادرست آن در داخل کشور است. این الگوریتم قادر به تعیین محدوده نهایی بهینه میباشد و این در حالی است که نخستین معرفیکنندگان روش در داخل کشور با یک برداشت اشتباه از الگوریتم آن را در زمره الگوریتمهای ناتوان در تعیین پیت بهینه دستهبندی کردهاند.